Research
As a Ph.D. student in applied mathematics I worked in the broad area of numerical methods for partial differential equation problems (PDEs).
The key idea is to work with PDE problems that can be viewed as a gradient flow of an energy, and design numerical schemes which satisfy a dissipative energy law at the discrete level similar to the continuous problem. Another aspect is balancing the accuracy of the numerical scheme with efficiency, since I have been focusing on real-world applications. Running simulations for these PDE problems in 3-dimensions requires a lot of computational resources.
I mainly focused on three projects.
Liquid Crystals: Numerical Schemes
Liquid Crystals (LCs) are unique materials that exhibit phase transitions between crystalline solid and isotropic liquid. The molecules that make up LCs are elongated, which causes them to align parallel to each other, and induces long range orientational order in the material. This ordering gives the material the macroscopic properties of a solid, but microscopic properties of a liquid.
LCs are anisotropic, meaning they have different properties when observed from different directions. This is why light shining through the material can make interesting patterns.
Many emergent technologies use LCs. For example, Liquid Crystal Displays (LCDs) use LCs to create images on a screen like TVs, monitors, e-books, and phones. LC Biosensors have been used to detect foreign objects inside of a cell using the optical anisotropy of the material, which can aid in medical diagnosis. Liquid Crystal Elastomers have been used to make smart fabrics, which can react to light or heat to change properties such as insulation. For instance, a LC sweater could be warmer when worn outside, and cooler when inside. Soft robotics using LCs is another interesting example where small robots are made with LCs that can preform actions in reseponse to light or heat.
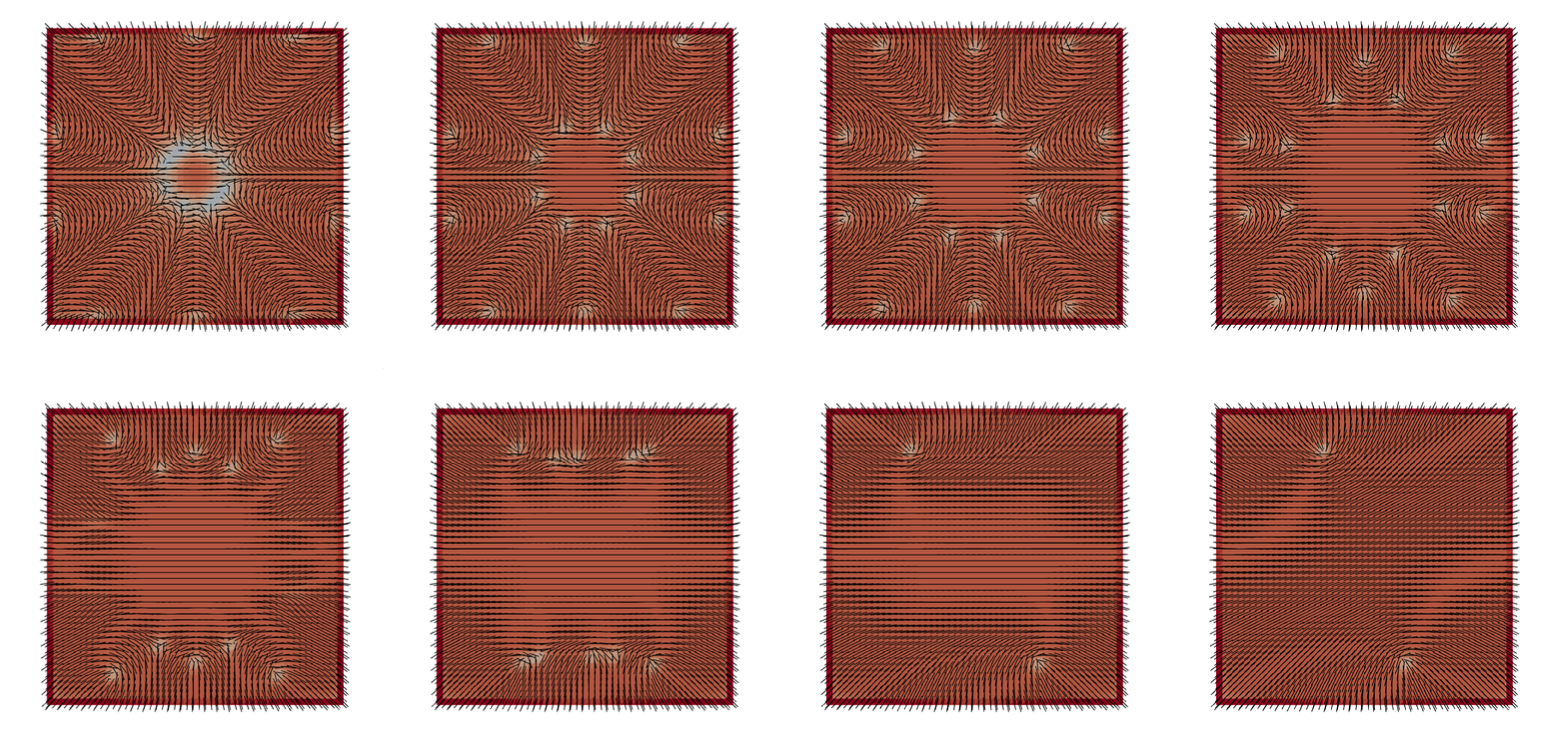
I have worked on building accurate, efficient, and energy stable numerical schemes for the Q-tensor model of LCs. This model can be viewed as a gradient flow of an energy which balances elastic and thermotropic contributions. and represents the average orientation of the molecules by the eigenvectors of a second order tensor Q.

Liquid Crystals: Interdisciplinary Research
In a series of projects, I have applied my work on Liquid Crystals to collaborative projects with material scientists at UNT to provide supporting simulation data for their experimental work.
The first project was focused on modeling the dynamics of defects inside small channels filled with LCs. Based on the boundary conditions and geometry of the channels we studied how stability of the defects.
Next, we worked on another phase of LCs called the Blue Phase. In this phase, the LCs form compicated geometric patterns of line defects inside the material. Our job was to investigate the deformation of line defects inside circular channels.

Recently, I have worked on modeling Cholesteric LCs. These materials are characterized by a balance of nematic ordering with a long range twist which is induced by molecules with high chirality.
Mixtures of Fluids: Phase-Field Modeling
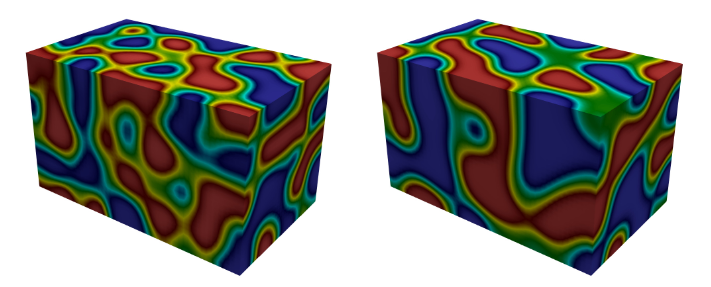
I have also worked on numerical methods for mixtures of several phases or fluids by investigating an extension of the Cahn-Hilliard model to several components. This model can be viewed as a gradient flow of an energy which balances elastic energy and a double well pontential. The unknowns are concentration variables which are assumed to transition continuously between phases through a thin interfacial region.
Several interesting problems in math and engineering can be investigated using the Cahn-Hilliard equation. Multi-phase fluid flow is a challenging problem which uses this model. Tumor growth is another interesting and important problem. As with the classical Cahn-Hilliard equation, which was used to model metal alloy manufacturing, the multicomponent model can also be used for ternary metal alloys. Associated with this problem is the dynamics of the spinodal decomposition, or the separation of phases which are originally well mixed.

Publications
-
Efficient Linear Schemes for a Penalized Ternary Cahn-Hilliard System
Justin Swain and Giordano Tierra
Submitted March 2025 -
Directed Self-Assembly of Chiral Liquid Crystals into Biomimetic Bouligand Structures in Thin Film with Superior Optical-Mechanical Properties
Tejal Pawale, Justin Swain, Mesonma Anwasi, David A. Czaplewski, Ralu Nana Silvia Divan, Giordano Tierra, and Xiao Li
Submitted February 2025
Code: Github -
Nucleation and Growth of Blue Phase 3D Cubic Structure under Continuously Changing Curved Boundary Conditions
Xiaowei Wang, Tejal Pawale, Justin Swain, David A. Czaplewski, Ralu Nana Silvia Divan, Giordano Tierra, and Xiao Li
Advanced Optical Materials
doi: 10.1002/adom.202402886 -
Linear Numerical Schemes for a Q-Tensor System for Nematic Liquid Crystals
Justin Swain and Giordano Tierra
Comp. Methods in App. Mechanics and Engineering
doi: 10.1016/j.cma.2024.117190 -
Dynamic Motions of Topological Defects in Nematic Liquid Crystals under Spatial Confinement
Tejal Pawale, Justin Swain, Mohammad Reza Hashemi, Giordano Tierra, and Xiao Li
Advanced Materials Interfaces
doi: 10.1002/admi.202300136 -
Genome Sequences of Streptomyces Phages Amela and Verse
Layton, S. R., Hemenway, R. M., Munyoki, C. M., Barnes, E. B., Barnett, S. E., Bond, A. M., Narvaez, J. M., Sirisakd, C. D., Smith, B. R., Swain, J., Syed, O., Bowman, C. A., Russell, D. A., Bhuiyan, S., Donegan-Quick, R., Benjamin, R. C., & Hughes, L. E.
Genome announcements
doi: 10.1128/genomeA.01589-15
Conference Presentations
-
Efficient Numerical Schemes for Multi-Component Mixtures of Fluids
Mini-symposium talk at SIAM CSE25
Fort Worth TX, March 2025 -
Efficient and Unconditionally Energy Stable Numerical Schemes for a Ternary Cahn-Hilliard System
Mini-symposium talk at SIAM TX-LA Sectional Meeting
Waco TX, October 2024 -
Efficient and Unconditionally Energy Stable Numerical Scheme for a Ternary Cahn-Hilliard Model
Poster presentation at UNT Research Day 2024
Denton TX, October 2024 -
Linear Numerical Schemes for a Q-Tensor Model of Nematic Liquid Crystals
Mini-symposium talk at SIAM TX-LA Sectional Meeting
Lafyette LA, November 2023 -
Energy Stable Numerical Schemes for Nematic Liquid Crystals
Poster presentation at SIAM Annual Meeting
Pittsburgh PA, July 2022 -
New Numerical Schemes for the Q-Tensor Model of Nematic Liquid Crystals
Poster presentation at SIAM TX-LA Sectional Meeting
Houston TX, November 2022